不良は発生していませんか? 工程能力は十分ですか😥?
工程能力指数は、工程変動による品質のバラツキが、規格幅に対しどんな状態かを示します。
工程能力指数によって工程能力が十分で、設計通りであるか? 不足しているか? がわかり
対策を打つことができます。😊
ここでは、工程能力指数を説明します。
バラツキの基礎「正規分布」
1-1 正規分布の表し方
平均値μ、標準偏差σ の正規分布を 「N(μ、σ2)」と表します。
左右対称の釣り鐘形です。
μ 平均値:分布の中心位置を表します。
σ2 分散:正規分布の広がり具合を表します。
標準偏差σ=√{∑(xi-μ)2/(n-1)}
σが大きいと横に広がる
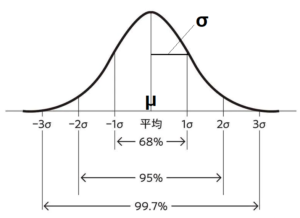
1-2 正規分布の性質
±σの間のデータが存在する確率は一定です。
±σは68.3%、
±2σは95.4%、
±3σは99.7% と同じです。
平均μ=0、標準偏差σ=1(分散1)の正規分布を標準正規分布 N(0,12)といいます。
①実際のデータ N(μ、σ2)
②中心値を μ から 0 に変更します。(μを引く)⇒ 上限規格値は x-μ となる。
③バラツキ σ を 1 に変更します。(σで割る) ⇒ 上限規格値は (x-μ )/σ となる。
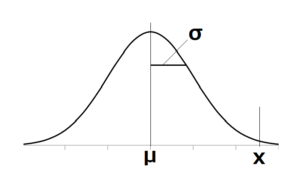
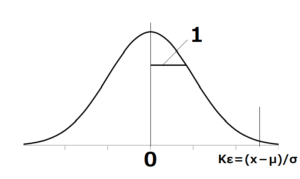
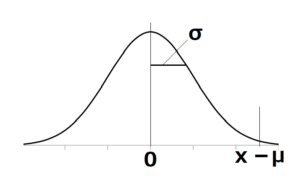
①実際の正規分布表 N(μ、σ2) ⇒ ②中心値をμから0にする。⇒ ③幅を σ → 1 にする
幅は変わらず (σで割る)
上限規格値はx 上限規格値はx-μ 上限規格値はKε=(x-μ)/σ
工程能力指数Cp、Cpk
●工程能力指数は、工程変動による品質のバラツキが規格幅に対しどんな状態かを示します。
3-1 工程能力指数 Cp (管理された理想の工程)
●品質のバラツキが適正か判断できます。
平均値を規格中心へ調整したら、Cp値まで工程能力が向上する という目安になります。
式は、規格の範囲を標準偏差の6倍で割ったものです。
Cp = (U-L)/6σ
U : 規格上限値、 L : 規格下限値、 σ : 標準偏差
●工程能力と不良率
| 規格幅 U-L | 工程能力 Cp | 不良率 | 備考 |
| 2σ=±1σ | 0.33 | 31.7% | ±1σの範囲に68.3%が含まれる |
| 4σ=±2σ | 0.67 | 4.55% | ±2σの範囲に95.4%が含まれる |
| 6σ=±3σ | 1 | 0.27% | ±3σの範囲に99.7%が含まれる |
| 8σ=±4σ | 1.33 | 0.006% 63ppm ppmは=1x10-6 | ±4σの範囲に99.99%が含まれる |
| 10σ=±5σ | 1.67 | 0.00006% 0.57ppm | ±5σの範囲に99.9999%が含まれる |
| 工程能力 Cp | 工程能力判断 | 工程能力の目安 |
| 1.67≦Cp | 十分すぎる | Cp=1.67:±5σ 不良率0.6ppm 管理の簡素化やコスト低減を検討する |
| 1.33≦Cp<1.67 | 十分足りている | Cp=1.33:±4σ 不良率63ppm 理想的状態であり、維持する |
| 1.0≦Cp<1.33 | 十分ではないが まずよい | Cp=1.0 :±3σ 不良率0.27% (千三つ) 工程管理を行い、統計的管理状態を保つ。 1.0に近づくと不良発生となるので注意する |
| 0.67≦Cp<1.0 | 不足している | Cp=0.67 :±2σ 不良率4.55% |
| Cp<0.67 | 非常に不足している | ±σ 不良率31.7% 品質保証ができない |
●工程能力Cpは、データのばらつき具合を示します。
製造工程は、工程能力 1.33≦Cp<1.67 が適しています。
規格の上下限値は±4σが適しています。
試作段階で適正公差への作りこみが大切です。
●工程能力Cpを上げる方法
1)ばらつきを下げる工程改善を行う
2) 公差を広げる設計検討を行う
3)検査により良品の選別を行う
3-2 工程能力指数 Cpk
ばらつきと中心値のずれが加味されます。
平均値が規格中心から離れている場合、規格片側の幅が小さい方を用いて計算する
Cpk = (U-x)/3σ または Cpk = (x-L)/3σ
U : 規格上限値、 L : 規格下限値、 σ : 標準偏差まとめ
0<Cpk<1 中心値がずれている。
Cpk=1 3σ内の範囲にあり、まずまず。
1<Cpk 1.33≦Cpkなら4σ内の範囲にあり安定している
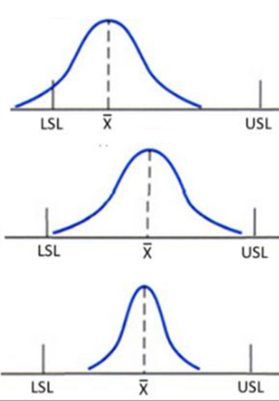
3-3 工程能力指数の評価
| 工程能力指数の関係 | 判定結果 |
| Cpk≒Cp 工程能力は十分有り | 問題なし |
| Cpk<Cp 工程能力は十分有り | 問題なし |
| Cpk<Cp Cpは十分あり Cpkは不十分 | 分布中心が規格中心から外れている |
まとめ
●工程能力 Cpk≧1.33(±4σ)が望ましい。
Cpk<1でも全数検査を合格すればよい。少量生産数の場合、全数検査して対応してもよい。
●工程能力を測定すると非常に厳しい公差、余裕がありすぎる公差の部品があります。
「余裕のある公差」「厳しい公差」の部品に分けてトータルで優れた製品を設計してください。
●試作にて 1.33≦Cp でも 1.33<Cpk の場合(平均値がずれている場合)
⇒量産までに工程能力を改善します。
バラツキσの変更は難しいですが、平均値μは比較的値を改善し易い。
⇒品質上問題ない場合は設計変更して許容します。
金型変更を要する場合、下手に手を入れると他の品質が悪くなる恐れがあります。
参考資料文献
栗山弘著 公差設計入門
最後まで見ていただき ありがとうございました。


